TN04-What is the dual-frequency modulation of CW-iToF?

According to the formula d_max = c/2f, it can be known that the lower the frequency, the greater the maximum value of the measurement distance, which is accompanied by the problem of reduced accuracy and precision or large jitter. On the contrary, the higher the frequency, the higher the accuracy and precision, but increasing the frequency will bring about the problem of decreasing the maximum measured distance of one cycle. One method of solving CW-iToF(Continuous Wave-indirect Time of Flight) range aliasing is dual-frequency measurement, where two different frequencies are used for the same measurement object and the true distance is determined from the results of the two measurements. Currently our CW-iToF camera is using high-frequency 120MHZ to improve the measurement accuracy and precision, and using low-frequency 20MHZ to calculate the current cycle number and then calculate the final true distance. Next, let us look at how to calculate it.

How to measure maximum detection distance by dual-frequency?

Assuming that the measured phase at a frequency of f_A is φ_A, the measured phase at a frequency of f_B is φ_B, the speed of light is c. Then the maximum measured distance of f_A is d_A=c/2f_A ,the maximum measured distance of f_B is d_B=c/2f_B.
The maximum distance is determined by the dual-frequency greatest common divisor f_E:

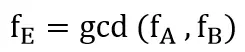
Convert f_A:f_B to two integer numbers that are prime numbers to each other M_A:M_B:

Suppose that φ_A corresponds to an aliasing number n_A(0 ≤ n_A ≤ M_A -1), φ_B corresponds to a aliasing number n_B(0 ≤ n_B ≤ M_B -1).
Coverts φ_A and φ_B the phase to within [0, 1]:

The true distance can be calculated as d_true =d_A ×(n_A + P_A) =d_B ×(n_B + P_B).
Take|d_A ×(n_A + P_A) – d_B ×(n_B + P_B)| to get the minimum value, solving for the corresponding n_A and n_B.Because

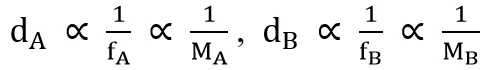
the solution of n_A and n_B can be converted into the following equation:

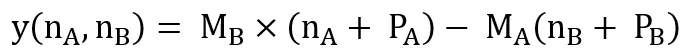
Therefore the formula for calculating true distance d_true is:

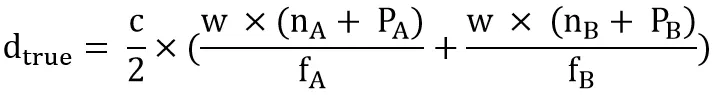
For example:
Suppose the two measurement frequencies f_A =30MHZ and f_B =40MHZ, the frequencies f_A measured distance is d_MA=4.0m, the frequencies f_B measured distance is d_MB=1.5m, the true distance under dual frequency is solved as follows:
The frequencies f_A maximum distance is d_A,

The frequencies f_B maximum distance is d_B,

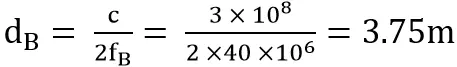
The dual-frequency greatest common divisor f_E = gcd(f_A, f_B) = 10MHZ,

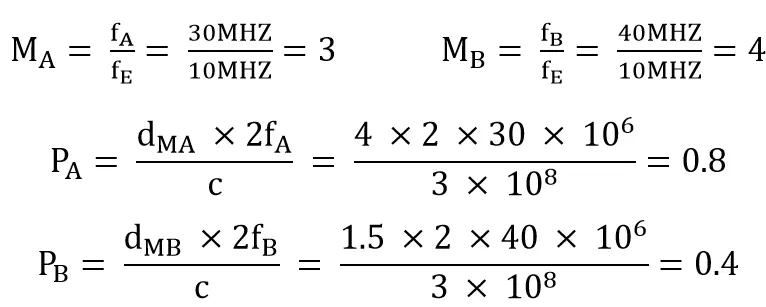
Minimum y(n_A, n_B) = M_B ×(n_A + P_A) – M_A ×(n_B + P_B) is obtained by calculating when n_A =1, n_B =2.
Finally get the true distance d_true = 5×(1 + 0.8 ) = 9m.

The theoretical maximum measurement distance and error rate of different frequency combination

The following table shows the maximum values of the high and low frequency ration:

High frequency(MHZ)	Low frequency(MHZ)	Theoretical maximum distance
100	15	30
100	45	30
100	65	30
100	10	15
100	30	15
100	70	15
100	20	7.5
100	60	7.5
100	80	7.5
100	25	6
100	50	3

	error rate/%	error rate/%	error rate/%
Distance/m	100MHZ&90MHZ	100MHZ&80MHZ	100MHZ&60MHZ
0.5	0	0	0
1.0	0	0	0
1.5	0	0	0
2.0	0.4	0	0
2.5	0.8	0	0
3.0	4.4	0	0
3.5	12.7	0.4	0.1
4.0	22.7	1.3	0.9
4.5	32.9	5	1.6
5.0	40.8	10.4	8.3
5.5	48.7	16	12.2
6.0	34.8	21.6	18.9
6.5	28	31.3	30
7.0	32.6	39	34.4